沈殿池

沈殿池とは、原水に含まれている浮遊物質などの固形物を沈降させて底にたまった泥を捨てる装置です。ここでポイントとなることは、底まで沈まなかった浮遊物は除去できないということです。つまり、非常に小さい粒子は沈む速度が遅いので、時間をかけなくては除去できません。

ここで、図を用いて除去率について説明していきます。下の図を見てください。三つの沈殿池のモデルが描かれています。これらは、左側から原水が流入し右側へ抜けていくという状況です。

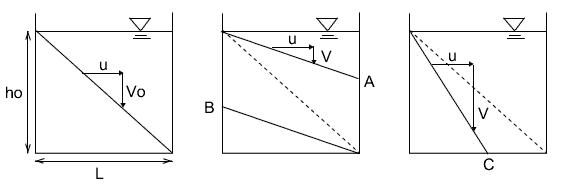
まず、左の図はこの沈殿池で計画されている大きさの粒子の沈殿していく軌跡が描いてあります。計画されている粒子は、速度$V_0$で沈降していき、流入時は水面近くにあったとしても右側に達したときには底に着く様子がわかります。計画された粒子は、除去率１００％と考えることができます。

真ん中の図は、左で考えた粒子よりも小さい粒子の軌跡を描いています。ここでの粒子は速度$V$で沈降していきます。流入時に水面近くにあった粒子は、底に達することができず　点A　までしか沈みません。つまり、Aより上の水は清涼な水で、Aより下にはまだ粒子が残った水になります。ここで考えた粒子の除去率は$V/V_0$です。流入時　点B　よりも下から流入した粒子は全て除去できます。

右の図は、左の図の粒子よりも大きな粒子の軌跡を描いています。この粒子は、流入時には水面近くにあっても　点C　に達する。除去率は１００％です。

以上が基本的な考え方です。では、沈降速度を求めてみましょう。沈降速度を求めるとはいっても、公式に値を代入していくだけなので簡単に求められます。$\rho _s$を粒子密度、$\rho$を流体密度、$d$を粒径、$\mu$を粘性係数として