ここでは、先ほどのフーリエの基本則を三次元で考えた上、固体温度の上がりやすさもあわせて考えます。固体の温度の上がりやすさは、中学校で勉強する比熱という指標で考えられます。比熱の単位は[J/K・kg]です。これは単位質量(1kg)の温度のを1℃上げるのに必要な熱量を示しています。
しかし、コンクリートの壁なんかをイメージすると、質量がわかることよりも体積の方がはかりやすいですよね?壁の重さをはかるより図面から体積を計算する方が断然早くできそうですよね?なので、比熱よりも容積比熱(heat capacity)として温度の上がりやすさを考えます。容積比熱は次の式で表すことができます。
容積比熱 $=c\gamma$
$c$と$\gamma$はそれぞれ比熱と比重量[kg/m3]を表しています。こうすることで、容積比熱の単位が[J/m3K]となり、比熱を体積で考えることができます。つまり、単位体積(1m3)の温度を1℃上げるのに必要な熱量を示しています。
では、容積比熱の説明も終わったところで今回の本題に入っていきます。まずは下の図を見てください。
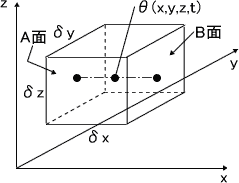
ここには、一辺の長さが$\delta x$、$\delta y$、$\delta z$の微小な直方体があります。その中心温度を$\theta$として、その時間変化$\left( \partial \theta / \partial t \right)$を考えていきます。
x軸と平行な方向での熱伝導を考えます。x軸と垂直な面であるA面の中心温度は、変化の割合が$\partial \theta / \partial x $で距離が$\delta x / 2$であることから次のように書くことができます。
したがって、面Aから$\triangle t$時間に直方体に流入する熱量は、フーリエの基本則と面積が$\delta y \delta z$であることから次のように書くことができます。
同様に面Bについても考えると、中心温度は次のようになります。
また同様に、面Bから$\triangle t$時間に直方体に流出する熱量は次のようになります。
以上から、直方体に蓄えられる熱量は面Aから中心への熱量と中心から面Bへの熱量の差をとって次のようになります。
これに対して、$\triangle t$時間の中心の温度上昇を$\triangle \theta$とすると、中心が得た熱量は容積比熱を考えると次のようになります。
先に熱流から求めた熱量と、今求めた熱量は等しいので次のように簡単にすることができます。
さらに、微小時間$\triangle t$を左辺に移項し、$\partial t$とすることで次のようになります。
ここで、右辺の係数は次のようにまとめられます。
これは、熱拡散率(thermal diffusivity)もしくは温度伝導率といって、温度が伝わる速度を表す物性値です。この値が大きいほど温度変化が早く、小さいほど温度変化が遅いことになります。
これで、x軸方向の熱流だけを考えた中心温度の時間変化が求められました。y方向、z方向も同様に求めることができるので全て合わせると次のようになります。
これが、三次元の熱伝導の微分方程式で、中心温度の時間変化は三方向の温度変化の二階微分の和に熱拡散率をかけたものだとわかります。
今回は、式を立てて微分方程式を導き、熱伝導の考え方を勉強しました。次は、この微分方程式に条件をつけて考えてみます。