連続の式とは、質量保存則のことで水の場合は非圧縮性、つまり密度が一定と考えていいので連続の式は体積保存の式として用いられている。その式の形は$\rho$を密度、$u$をx方向の流速、$v$をy方向の流速、$w$をz方向の流速として
$\frac{\partial \rho}{\partial t} + \rho \left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \right) = 0$ (二次元)
$\frac{\partial \rho}{\partial t} + \rho \left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} \right) = 0$ (三次元)
となり、$\rho$を一定とすると
$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$ (二次元、非圧縮)
$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z} = 0$ (三次元、非圧縮)
と表すことができる。さらに、管の中を流れる水に対する連続の式は、$Q$を流量、$A$を管の断面積、$v$を流速として
$Q=Av=Const.$
と書ける。
では、一番上の二次元の連続式を導いてみましょう。
質量保存の式なので、基本的な考え方は辺の長さが$dx$、$dy$の長方形に関して (質量の変化量)=(流入する量)-(流出する量) とすることです。
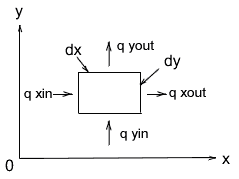
まず、左辺から考えてみましょう。質量の変化量は
$\frac{\partial}{\partial t}\left( \rho dx dy \right)$
と書けます。この式のカッコ内は (密度)×(面積) で質量を求めています。カッコの前についているものは、“カッコ内のものが時間で変化する量”を表しています。
次に、右辺を考えます。図の長方形の中心におけるx方向の流速を$u$、y方向の流速を$v$とします。$u$も$v$も少しずつ変化しているので、左の辺での流速は
$u-\frac{\partial u}{\partial x} \frac{dx}{2}$
と書けます。この式の意味していることは、左の辺が中心から $(-dx/2)$ 進んだ位置にあるから、流速は$u$よりも (1mあたりの$u$の変化量)×$\left(-dx/2\right)$ だけ大きい値になるということです。(偏微分がわからない人は…勉強してください(^^ゞ)
他の辺における流速も同じように考えると
$v-\frac{\partial v}{\partial y}\frac{dy}{2}$ (下の辺)
$u+\frac{\partial u}{\partial x}\frac{dx}{2}$ (右の辺)
$v+\frac{\partial v}{\partial y}\frac{dy}{2}$ (上の辺)
となります。流速が求まれば後は簡単です。x方向の流速に$dy$をかければ流量になります。また、y方向の流速に$dx$をかけても流量になります。結局、流量は
$q_{xin}+q_{yin}-q_{xout}-q_{yout}$
$= \rho \left( u-\frac{\partial u}{\partial x}\frac{dx}{2} \right) dy + \rho \left( v- \frac{\partial v}{\partial y}\frac{dy}{2} \right) dx$
$- \rho \left( u + \frac{\partial u}{\partial x}\frac{dx}{2} \right) dy - \rho \left( v + \frac{\partial v}{\partial y}\frac{dy}{2} \right) dx$
とまとめることができます。
上で考えた左辺と右辺をつなげれば
$\frac{\partial}{\partial t}\left( \rho dx dy \right)$
$= \rho \left( u - \frac{\partial u}{\partial x}\frac{dx}{2} \right) dy + \rho \left( v- \frac{\partial v}{\partial y}\frac{dy}{2} \right) dx$
$- \rho \left( u + \frac{\partial u}{\partial x}\frac{dx}{2} \right) dy - \rho \left( v + \frac{\partial v}{\partial y}\frac{dy}{2} \right) dx$
となり、整理すると($dxdy$で割って同じ項を消していく)
$\frac{\partial \rho}{\partial t} + \rho \left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} \right) = 0$
が得られます。