マルサス的成長を考える前に、個体数の増加を考えていきます。まず、考える環境は食物や温度、水、空間に制限がなく最適な状態です。ここで、出生率a、死亡率bを考えると個体数Nの増加率は
$\frac{dN}{dt} = aN - bN = \left( a-b \right) N$
と表すことができます。 a-b は増加率rと考えることができるので、これを用いると
$\frac{dN}{dt} = rN$
と表すことができます。これを時間$t$で積分すれば、ある時間における個体数が求められるはずです。積分すると
$\int \frac{1}{N}dN = \int rdt$
$N\left(t\right)= e^{rt+C}$
になります。ここで$C$は積分定数ですが、最初の個体数を決めれば決定するので最初の個体数を$N_0$とすると
$N\left(t\right) = N_0 e^{rt}$
が得られます。今の状態では増加率は出生率と死亡率に依存して変化します。しかし、年齢構成が安定化したとき一定の値をとるようになります。このときの$r$を内的自然増加率といい、生物種によって決まった大きさを持ちます。また、その種の増加能力を示す指標でもあります。このような成長を妨げる要因がない個体数の増加をマルサス的成長といいます。
サラッと終わることができたので、ついでにロジスティック成長式もやってしまいましょう(^^)
ロジスティック成長式とはマルサス的成長よりも少し現実的な条件です。なにが変わるのかというと、環境の変化を考慮に入れようということです。環境の変化とは天候が変わったり、病気が発生したり、生活空間が限られて食料や水が不足したり、老廃物による環境汚染もあるということです。
以上の影響をまとめて環境抵抗とします。環境抵抗を環境収容力$K$として式にふまえると
$\frac{dN}{dt} = rN\left(1-\frac{N}{K} \right)$
というように表現できます。グラフのほうがわかりやすいと思うので、グラフで表現すると下のようになります。
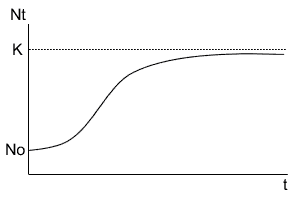
このグラフは$N_0$から始まって徐々に増えていきます。しかし、環境収容力$K$に近づくにつれて増加速度はゆっくりになっていきKに漸近していくようになっています。マルサス的成長はひたすら増えていくだけだったので、個体数に限界のあるロジスティック成長は現実に近いといえるでしょう。また、現に微生物の培養においてはこの式の結果がよく当てはまっています。