前回は、定常熱伝導と非定常熱伝導について解説を行いました。ここからは、定常熱伝導に限った話を進めていきます。
定常での熱伝導方程式は、$\partial \theta / \partial t = 0 $とすることで求められました。ここでは、話をさらに簡単にして一次元の問題を扱います。一次元の定常熱伝導方程式は次のように表すことができます。
これは、積分すると簡単に解くことができるので、積分すると次のようになります。
ここで、$r_1$、$r_2$は積分定数です。このようにただの一次式になります。つまり、定常状態での温度分布は下の図のように直線で表すことができるということです。
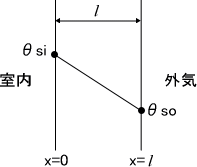
この図は、室内側の表面温度を$\theta_{si}$、外気側の表面温度を$\theta_{so}$としたときの厚さ$l$の壁の温度分布を表しています。このとき、$r_1$、$r_2$が求められ次のようになります。
また、この壁を抜けていく熱量$q$はフーリエの法則から求めることができ、次のように表すことができます。
ここで、$\lambda / l = C$ とし、$C$は熱コンダクタンスといいます。コンダクタンスとは通し易さを意味しているので、今の場合熱の通し易さということになります。そして、この$C$の逆数 $1/C$ は、通し易さの逆ということで、熱抵抗 $R$ といわれます。
ここまで、単層の壁を考えましたが、次は複層の壁を考えます。複層でも先ほどと同じように定常な状態を考えれば、壁を通過する単位面積当たりの熱量 $q$ はどこも一定であるとなります。つまり、各層の熱コンダクタンスを$C_1$、$C_2$、$C_3 \cdots C_n$とすれば、次のように書くことができます。
結局は、どの層を通過する単位面積当たりの熱量は同じということです。それを図にすると下の図のようになります。
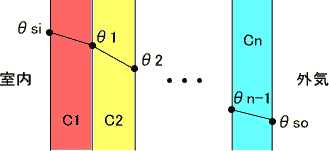
各層の傾きは、熱コンダクタンスの大きさによってきまるので変化していることがわかります。ここからさらに、上の連立方程式から$\theta _1$から$\theta _{n-1}$までを消去すると次のようになります。
ここで、$\frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n}$ と $C$ をまとめると次のように簡単な形にすることができます。
これは、単層のときの式と同じ形ですね。したがって、室内側の温度と外気側の温度がわかっていれば、定常状態のときの熱伝導量を熱コンダクタンスをまとめることで計算できます。次回は、実際の熱抵抗などを用いて複層壁の熱コンダクタンスを求めてみましょう。