高校のときに物理を勉強した方は、ニュートンの第二法則を覚えているでしょう。よく出てきた $F=ma$ ってやつです。これが、固体を対象とした物理での運動方程式でした。流体を対象とした物理にも運動方程式が存在します。それが、ここの題名のオイラーの運動方程式です。
では、とりあえずオイラーの運動方程式がどのようなものか見てみましょう。オイラーの運動方程式は、X、Y、Zを質量に比例してx、y、z方向それぞれに作用する加速度(重力や遠心力)として
$\frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = X - \frac{1}{\rho} \frac{\partial p}{\partial x}$ (2次元、x方向)
$\frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} = Y - \frac{1}{\rho}\frac{\partial p}{\partial y}$ (2次元、y方向)
3次元では
$\frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} + w\frac{\partial u}{\partial z} = X - \frac{1}{\rho}\frac{\partial p}{\partial x}$ x方向
$\frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} + w\frac{\partial v}{\partial z} = Y - \frac{1}{\rho}\frac{\partial p}{\partial y}$ y方向
$\frac{\partial w}{\partial t} + u\frac{\partial w}{\partial x} + v\frac{\partial w}{\partial y} + w\frac{\partial w}{\partial z} = Z - \frac{1}{\rho}\frac{\partial p}{\partial z}$ z方向
のようになります。以上は圧縮性の流体にも適用できる形です。非圧縮性に限定すると$\frac{\partial u}{\partial t} + \frac{\partial u^2}{\partial x} + \frac{\partial uv}{\partial y} + \frac{\partial uw}{\partial z} = X - \frac{1}{\rho}\frac{\partial p}{\partial x}$ x方向
$\frac{\partial v}{\partial t} + \frac{\partial uv}{\partial x} + \frac{\partial v^2}{\partial y} + \frac{\partial vw}{\partial z} = Y - \frac{1}{\rho}\frac{\partial p}{\partial y}$ y方向
$\frac{\partial w}{\partial t} + \frac{\partial uw}{\partial x} + \frac{\partial uw}{\partial y} + \frac{\partial w^2}{\partial z} = Z - \frac{1}{\rho}\frac{\partial p}{\partial z}$ z方向
となります。以上の式は非定常な流れにおいても適用できます。また、実際の世界においては、容器に入った水や地震が起こったときなどを考えない場合、$X=Y=0$、$Z=g$ として考えます。
では、このオイラーの運動方程式を導いてみましょう。
下の図のように、AからBに流体が移動する現象を考えます。圧力は連続の式のときの流速と同じようにして、上の辺、右の辺に作用する大きさを求めます。今回の流速は位置がx方向にもy方向にも変化しているため、それぞれの方向に対する変化量を加えなくてはいけません。
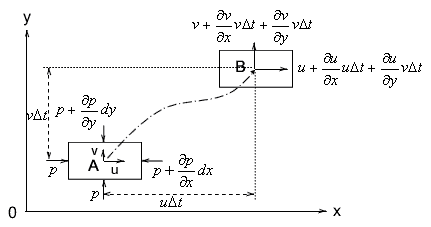
長方形の辺の長さは$dx$、$dy$です。目的は運動方程式なので、まずAに作用する力を考えましょう。 $m$ を質量として
$F_x = pdy - \left( p+\frac{\partial p}{\partial x}dx \right) dy + mX$
$F_y = pdx - \left( p+\frac{\partial p}{\partial y}dy \right) dx + mY$
$mX$、$mY$は$X$、$Y$がx、y方向の加速度だから、ニュートンの運動方程式から導かれたものです。これでx、y方向の力が求められました。
次に、質量はわかっているので加速度を求めます。加速度は (Bの流速)-(Aの流速) を計算して$\triangle t$で極限をとれば求められます。したがって
$\alpha _x = \lim _{\triangle t \to 0} \frac{u+\frac{\partial u}{\partial x} u\triangle t + \frac{\partial u}{\partial y} v\triangle t - u}{\triangle t} = u \frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}$
$\alpha _y = \lim _{\triangle t \to 0} \frac{v+\frac{\partial v}{\partial x} u\triangle t + \frac{\partial v}{\partial y} v\triangle t - v}{\triangle t} = u \frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}$
と求められます。非定常流ではx、y方向に$\partial u/\partial t$、$\partial v/\partial t$を加えないといけません。ここで、$m=\rho dxdy$
とわかっているので、これを代入して $F=ma$ となるようにすると$\frac{\partial u}{\partial t}+ u \frac{\partial u}{\partial x} + v \frac{\partial u}{\partial y} = X - \frac{1}{\rho} \frac{\partial p}{\partial x}$
$\frac{\partial v}{\partial t}+ u \frac{\partial v}{\partial x} + v \frac{\partial v}{\partial y} = Y - \frac{1}{\rho} \frac{\partial p}{\partial y}$
が得られます。