ここでは、分子拡散だけによる拡散方程式を扱います。まずは下の拡散方程式を見てください。
$\frac{\partial C}{\partial t} = D\frac{\partial ^2 C}{\partial x^2}$ 一次元分子拡散方程式
$\frac{\partial C}{\partial t} = D\left( \frac{\partial ^2 C}{\partial x^2} + \frac{\partial ^2 C}{\partial y^2} \right)$ 二次元分子拡散方程式
$\frac{\partial C}{\partial t} = D\left( \frac{\partial ^2 C}{\partial x^2}+\frac{\partial ^2 C}{\partial y^2}+\frac{\partial ^2C}{\partial z^2} \right)$ 三次元分子拡散方程式
次元が上がるにつれて、項が一つずつ増えていきます。$C$は濃度を、$D$は分子拡散係数[m^2/s]を表しています。
この式を導くにはフラックスという考えかたを導入する必要があります。なので、フラックスの説明をしてから導出してみましょう。
まず、フラックスとは言葉で説明すると単位時間、単位面積当たりに通過する物質の量のことをいいます。しかし、これではわかりづらいので図と式を用いて説明しましょう。下の図を見てください。
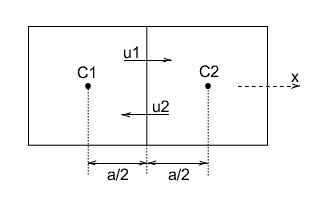
左の部屋と右の部屋の物質のやり取りを考えます。このとき、物質のやり取りは境界においてのみ行われると考えます。左の部屋の濃度を$C_1$、右の部屋の濃度を$C_2$として左から右に向かう物質の速度を$U_1$、逆を$U_2$とします。右向きを正とすると、移動量は
$C_1 u_1 - C_2 u_2$
と書くことができます。これが質量フラックスです。このままだと4つの数を決めないとフラックスが求まらないので表現を簡単にしていきます。
今は分子運動を考えているので物質の移動速度はどこも等しいと考えられ、$U_1=U_2=U_m$ とすれば
$\left( C_1 - C_2 \right) u_m$
となります。
ここで、$C_1$と$C_2$は距離$a$だけ離れた二点なので、その濃度はテイラー展開を利用した
$C\left( x+a \right) = C\left( x \right) + \frac{\partial C}{\partial x} a$
という形から、$C_1$と$C_2$の関係は$C_2 = C_1 + \frac{\partial C}{\partial x} a$
と表現できます。
分子の平均自由移動距離を$l_m$とすると
$a\simeq l_m$
と考えていいので、結局質量フラックス($J_x$とおきます)$J_x = \left( C_1 - C_2 \right) u_m$
は上で求めたものを代入していくと$J_x = - \frac{\partial C}{\partial x} l_m \cdot u_m$
になります。さらに簡単にするために$u_m \cdot l_m$は分子拡散係数$D$と等しいので$J_x = -D \frac{\partial C}{\partial x}$
になります。この形が分子拡散の質量フラックスを表しています。マイナスがついているのは、濃度の傾きと物質の移動方向が逆向きになるからです。つまり、濃度勾配が正であればフラックスは左向きで、濃度勾配が負であればフラックスは右向きになります。
次に、拡散方程式を求めていきます。フラックスがわかっていれば簡単に導くことができます。下の図を見てください。
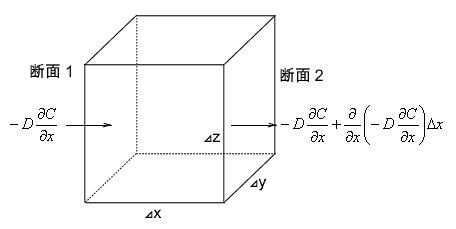
上のような箱を考えたとき、この箱を出入りする物質のフラックスを考えます。とりあえず簡単な一次元を考えてみましょう。一次元では左から入ってきて右に抜けていく状態を考えます。左の断面から入ってくるフラックスを
$-D \frac{\partial C}{\partial x}$
とおいたとき、右の断面から出て行くフラックスは$-D \frac{\partial C}{\partial x} + \frac{\partial}{\partial x} \left( -D\frac{\partial C}{\partial x} \right) \triangle x$
と考えることができます。これはよく使っている考え方なので大丈夫ですよね?わからない方は水理学を復習してください。上の二式に断面積$\triangle y \triangle z \triangle t$をかけて差をとれば$\left[ -D\frac{\partial C}{\partial x} \left( \triangle y \triangle z \triangle t \right) \right] - \left[ \left(-D \frac{\partial C}{\partial x} - D\frac{\partial ^2 C}{\partial x^2} \triangle x \right) \left( \triangle y \triangle z \triangle t \right) \right]$
となり、これを簡単にすると$D\frac{\partial ^2 C}{\partial x^2} \triangle x \triangle y \triangle z \triangle t$
が得られます。これは$\triangle t$秒間に変化する箱の中の物質量です。
上の式に対して、濃度$C$から直接変化量を求めることもできます。それは、
$\left[ C\triangle x \triangle y \triangle z + \frac{\partial \left( C \triangle x \triangle y \triangle z \right)}{\partial t} \triangle t \right] - \left( C \triangle x \triangle y \triangle z \right)$
という式で計算できます。これを簡単にすると$\frac{\partial C}{\partial t}\triangle x \triangle y \triangle z \triangle t$
になります。これも$\triangle t$秒間に変化する箱の中の物質量なので、二式を等号でつなぎ整理すると$\frac{\partial C}{\partial t} = D \frac{\partial ^2 C}{\partial x^2}$
という一次元の拡散方程式が得られます。この式を二次元、三次元と拡張すれば、二次元、三次元の拡散方程式が得られます。