ロトカとヴォルテラの競争方程式とは、ロジスティック式をさらに発展させたものでこの方程式を利用することで2種の動物が共存可能かどうかを判別することができます。競争方程式は種1と種2それぞれについて一つずつ式を与え比較します。その式は
さて、この式は実際に解いてみるわけではなく、グラフ化してその傾きを見ていきます。微分方程式からグラフ化というのは困難なので、条件を考えてグラフにできる形にします。その方法は$dN/dt=0$として求めていきます。$dN/dt=0$は、個体数が安定化した状態を考えたいからです。$dN/dt=0$は$N$が変化しなくなる状態なので、結局安定化した状態ということです。$dN/dt=0$として式を整理すると種1の式からは
$N_1$と$N_2$を軸としたグラフを考えると4通りのグラフになります。$K_1$と$K_2/a_{21}$、$K_2$と$K_1/a_{12}$のどちらが大きいのかで決まってきます。ここで注目することは「どこに収束するのか」ということです。どこに収束するかで共存などの判断ができます。判断する基準は、左右方向にはx軸、上下方向にはy軸に注目します。左右方向には$K_1$の方へ、上下方向には$K_2$の方へ収束していきます。つまりは、左右方向には青い直線のほうに、上下方向には赤い直線の方に向かいます。
(1) $K_1/a_{12}>K_2$ かつ $K_2/a_{21}>K_1$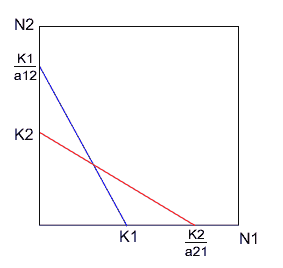
左右方向には青い方へ、上下方向には赤い方へと考えると、二直線の交点に収束することがわかります。これは、種1、種2ともにある個体数存在するということなので、この2種は共存できます。条件式を変形させると $K_1>a_{12}K_2$ と $K_2>a_{21}K_1$ なので種1の環境収容力の個体数と種2が環境収容力に達したときに種1を減少させる個体数を比較したときに種1の環境収容力の方が大きいということと、種2の環境収容力の個体数と種1が環境収容力に達したときに種2を減少させる個体数を比較したときに種2の環境収容力の方が大きいということを意味しています。
(2) $K_1/a_{12} < K_2$ かつ $K_2 /a_{21}< K_1$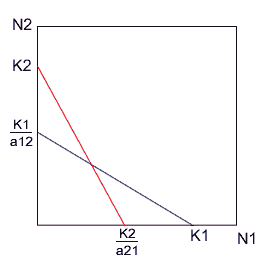
ここでも、同様に考えて左右方向は青、上下方向は赤と考えると、x軸の$K_1$の点もしくはy軸の$K_2$の点に収束することがわかります。これは、どちらか一方の種が生き残ることです。ここでも、条件式を変形すると $K_1 < a_{12}K_2$ と $K_2 < a_{21}K_1$ なので減少させる量の方がどちらも上回っているということがわかります。
(3) $K_1/a_{12}>K_2$ かつ $K_2/a_{21}< K_1$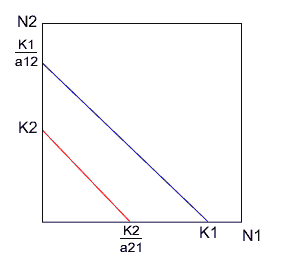
同様に考えてください。すると、x軸の$K_1$に収束することがわかります。条件式を見ると、種1が種2を減少させる個体数は種2の環境収容力よりも大きく、種2が種1を減少させる個体数は種1の環境収容力よりも小さいことがわかります。
(4) $K_1/a_{12}< K_2$ かつ $K_2/a_{21}>K_1$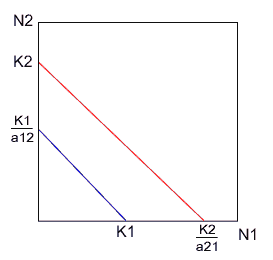
ここでは、y軸の$K_2$に収束することがわかります。条件式は、(3)と逆になっているはずです。
以上のようにしてロトカとヴォルテラの競争方程式を利用することができます。ポイントは方程式を一次関数の形に変えて見やすくすること、描いた4種類のグラフを見てどこに収束するのか判断することです。左右方向にはK1の方へ、上下方向には$K_2$の方へと覚えていれば簡単にできるでしょう。