ベルヌーイの定理は、粘性のない流体(完全流体)で定常流(流れが時間とともに変化しない流れ)でのみ適用できます。ある高さ$z$[m]の点において、圧力を$p$[N/m^2]、流速を$v$[m/s]としたとき
$\frac{p}{\rho g}+z+\frac{v^2}{2g}=Const.$ [m]
のように表現できるというのが、ベルヌーイの定理です。また、第1項を圧力水頭、第2項を位置水頭、第3項を速度水頭と呼び、(当然ですが)すべて単位が[m]です。 下の図は、1、2という2点でベルヌーイの定理を適用した例です。2点での断面積について、$ A1 < A2 $ とすると、連続の式($Q=Av=Const.$)から $ v1 > v2 $ となることがわかります。
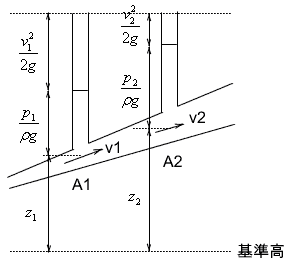
ベルヌーイの定理が高さmで表されているメリットは、上の図のようにベルヌーイの定理のそれぞれの項がその高さで表わすことができることです。1、2どちらの点においても、水頭の合計は変わらず、流速が遅くなった分だけ液面からの高さが少なくなっていることが確認できます。
ただ、この定理に違和感を覚える方もいるかと思います。それはこの定理をを利用する上で注意しなくてはならないことにもつながりますが、エネルギーの損失が全く考慮されていないということです。実際の現象では、途中でエネルギーの損失があるため水頭の合計が常に一定となることはありません。それはエネルギー損失を考慮しなくてはならないのですが、エネルギー損失についてはまたの機会で(^^)