ベルヌーイの定理の応用として、ここでは、ピトー管、ベンチュリ管、マノメーターを組み合わせたベンチュリーメーターの例を挙げたいと思います。まず最初にピトー管の説明をします。下の図に示しているのがピトー管です。二重管となっていて、A、Bの位置には穴が開おり、流速を測定することができる器具です。

左から右に向かって一様な流速vがあるとすると、穴AとBの位置における違いは流れに対して直角に穴が開いているか、平行に穴が開いているかということです。流れに直角に穴が開いているAにつながっている方は、一様流の流速の影響を受けて中の水位が高くなり、Bの方は一様流の影響がなく、ピトー管の外と水位が等しくなります。この水位差$\triangle H$で流速を測定することができます。
まず、AとBにベルヌーイの定理を適用すると次の式が得られます。
左辺がA、右辺がBです。AもBもほぼ等しい高さにあるので、圧力は同じだけ働きます。したがって、圧力$p$も基準面からの高さ$H$も同じ値になります。しかし、A点は流れの影響を受けるため流速の項が含まれます。その分だけ、水面が持ち上がることになります。
結局、上の式を整理すると次の式が得られます。
これで水位差$\triangle H$から流速が求めらることがわかりました。このピトー管は、現在でも管内の流速を知るためなどに使われているようです。
次は、ベンチュリ管とマノメーターを組み合わせたベンチュリーメーターについて説明します。下の図に二通りのベンチュリーメーターを示します。
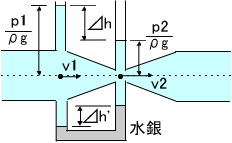
上に二本伸びているマノメーターと下にU字型に伸びているマノメーターのそれぞれで使用しますので、通常、どちらかがあれば使用可能です。これも先程のピトー管と同じく流量を測定するために利用します。まずは、上側から示していきます。
左側の$v1$の地点を1、右側の$v2$の地点を2とすると、1では$p1/\rho g$だけ水面が上がり、2では$p2/\rho g$だけ水面が上がります。(連続の式から断面が小さくなる分だけ流速が速くなり、速くなった分だけベルヌーイの定理から圧力が下がります。)したがって、水位差$\triangle h$を用いて次の式のようにまとめることができます。
次に、1と2ではエネルギーは保存されるので、ベルヌーイの定理を適用すると次の式が得られます。
また、1と2に連続の式を適用すると次の式が得られます。
以上の3式を連立させてpを消去して、$v2$について解くと次の式が得られます。
したがって、流量$Q$は次のようになります。
これで流量は、水位差と断面積から求められることがわかりました。上部マノメーターを使用したベンチュリメーターの説明は以上になります。最後に、下部マノメーターを使用したベンチュリーメーターです。これも基本的な部分はさきほどと全く同じです。
今回のマノメーターは下向きに管が出ています。その中には水銀などの水よりも比重の大きな流体が入っています。比重の大きな流体が入っている場合、圧力水頭差$\triangle h$は水銀面の高さの差$\triangle h'$を用いて次のように表すことができます。(簡単にわかると思うので、自分で確認してみてください。)
このように、$\triangle h$よりも小さな$\triangle h'$を測定することで流量を知ることができます。これは、流量が小さい場合は水位差が出にくく、見難くなるため不利になります。しかし、流量が大きい場合は、小さな水位差で測定が可能となるため有利に働きます。
これで、流速を測るピトー管、流量を測るベンチュリ管、マノメータの説明を終わります。