まずは、波の基本から始めます。下の図を見てください。この図の波は正弦波と呼ばれる波を示しています。正弦波とは、波が時間的にも空間的にも周期性のある波のことをいいます。また、凸になっている部分を波の山もしくは波の峰、凹になっている部分を波の谷といいます。
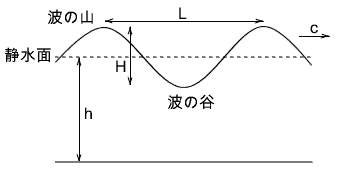
図にあるように、一周期の波の長さを波長Lといいます。波の速さを波速$c$、波の山と波の谷の鉛直距離を波高$H$、静水面から水底までの鉛直距離を水深$h$といいます。波の山から次の山の位置まで移動するのにかかる時間を周期$T$といいます。
上で挙げた々を組み合わせて特性量が表現されます。振幅$a$は $a=H/2$ で、波速$c$は $c=L/T$ で、波形勾配は $H/L$ で、相対水深は $h/L$ で、波数$k$は $k=2\pi /L$ で、角周波数$\sigma$は $\sigma=2\pi /T$ で表すことができます。これらの特性量はよく用いられるので、しっかり覚えていてください。
波の分類波には様々な分類方法があります。周期によって分類すると、表面張力波、風波、うねり、長周期波、津波、気象潮、潮汐と分けられます。また、規則的な波かどうかで、規則波と不規則波という分類ができます。波の形を三角関数で表すことができるかどうかで正弦波と非正弦波、波が進むかどうかで進行波と定在波、相対水深が小さい順に極浅海波、浅海波、深海波と分けられます。何に注目するかでその波の名前が決まるので、波の名前をつけるときにはどの性質に注目しているのかはっきりさせておく必要があります。
海岸工学では、波を微小振幅波と見て考えます。微小振幅波とは、振幅が非常に小さいと仮定した波のことで計算を単純化して考えることができます。単純化するとはいっても、ある程度の誤差を許容すれば波高が相当大きな波にも適用することができます。