ベルヌーイの定理(Bernoulli's theorem)の演習

ベルヌーイの定理を用いたよくある問題演習をします。ここでは単純なトリチェリの定理とそれに関連した縮流係数について説明していきます。

まずはトリチェリの定理です。トリチェリの定理では下の図のような水槽からの流出を考えます。このとき、水槽の水面位置が一定である場合に流出する流速を求めます。

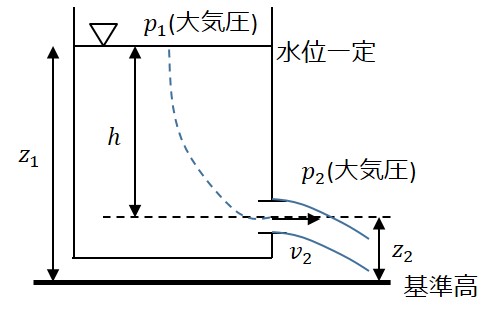
水槽の水面と流出口との間にベルヌーイの定理を適用します。すると一般に次の式が得られます。

ここで、水面位置が一定であることから$v_1=0$、大気圧であることから$p_1=p_2=0$であることがわかります。さらに$v_2$について整理すると次の式が得られます。

この式中の$z_1-z_2$は流出口と水槽内の水面高さの差と等しく$h$であるため、結局、次の式になることがわかります。

トリチェリの定理は、流出口の流速は水位差の平方根に比例して求められるというものです。

次の縮流係数（縮脈係数）について説明します。縮流係数は下の図に示すようなトリチェリの定理の流出口付近を考えます。

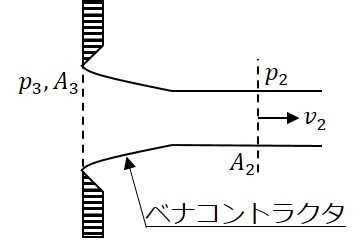
ここで、左側が水槽内部を示していると考えてください。このような流出口を持つ場合に、水槽側壁面に沿った流れ（流線）はさきほどのトリチェリの定理の図のように考えると直角に流れが曲がることになってしまいます。流れの向きが変わるということはなんらかの外力を受けるということなので、動きを直角に変えるような外力は考えられず徐々に向きを変えるような流れを考える必要があります。

実際には図に示すとおり流出口から徐々に細くなるような流れになります。この部分（ベナコンストラクタ）の流れは$v_2$に比べて少し流速が遅く、$p_2$（大気圧）より少し圧力が高い状態となり、流れの中心から外に向かう力が働いていると考えられます。この力が円運動の求心力のように働き、徐々に流れの向きを変えていきます。このような流出水の断面形状の変化を考慮するために縮流係数$C$が導入されます。縮流係数自体は単純なもので、$C=A_2/A_3$の断面積比で表されます。